BPC Insights – Revisiting Bond Market Fundamentals
- Doug Burns

- Oct 2, 2024
- 4 min read
Most people tend to think about stocks when considering financial markets. Stocks tend to be the “growth engines” of financial portfolios over long periods of time, albeit with volatility and risk of loss. They are easy to understand as they represent ownership in companies and get much of the media’s attention. On the other hand, a less understood market is the fixed income market, which is a much larger market (by capitalization) than the stock market. This article will hopefully peel back the onion layers on the fixed income market and give you a better understanding on what bonds are and how they behave.
Bonds are financial instruments that represent loans to entities. These entities could be the U.S. Government, corporations, or municipalities, to name a few. Much like a mortgage, the entity will borrow money with a promise to pay this money back in the future. Over this period, the lender will usually receive interest from the borrower to pay for the use of their money. Unless there is an inability of the entity to pay back the money, the lender will know how much they expect to earn over the life of the bond. The following example of a hypothetical bond will show how prices change with a changing interest rate environment:
On January 1st, 2025, I purchase a $1,000 plain vanilla three-year bond from Microsoft with a coupon rate of 5%. Typically, bonds pay their interest semiannually, so I would expect to receive $50 per year ($25 every six months) and then be paid back my $1,000 after the three years is up. Ignoring reinvestment of the interest payments, I would expect to earn 5% each year for three years.
Where things tend to get confusing is what happens when the prevailing interest rate in the market changes. To demonstrate, let’s continue to use the Microsoft bond example above. The terms of the bond are set, but let’s assume a year has passed and Microsoft is now issuing $1,000 two-year bonds that have a 6% coupon rate, because it reflects a changed interest rate environment.
Because I could now buy a bond that will mature at the same time as my original bond, but it pays a higher coupon rate, my original bond is worth less than I paid for it. In fact, when doing the calculations, on Jan 1, 2026, I would expect the original bond to be worth $981.41 which equates to a 1.9% drop in price.
Now it is important to remember that although my bond is worth 1.9% less, I still received the $50 interest payment, which would be a total return of 3.1%.
Fast forward another year and Microsoft is offering $1,000 one-year bonds with a 4% coupon rate because interest rates dropped. Now my 5% original bond with a year to maturity should be worth more than this new issuance. The price of my bond should equate to $1,009.71. Over this second year, I would have received a 5% coupon and price appreciation of 2.9%. The total return over this year would be 8%.
After the last year, we are going to be paid back the original $1,000, and the total return for year 3 should be 4%.
Again, if interest rates hadn’t changed at all over the life of the bond, we would have expected to return 5% per year.
The chart below shows the calculated return of the hypothetical bond:
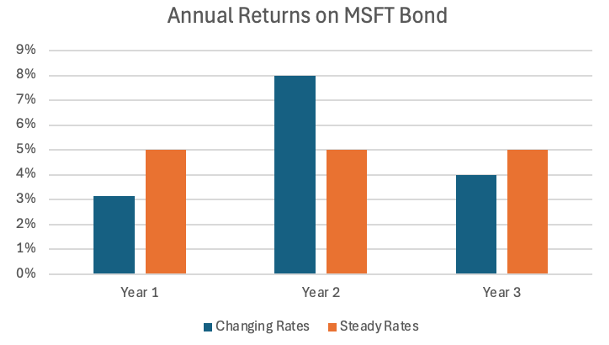
Mathematically, the return of the bond in the changing interest rate environment averages 5% per year, which is the same that we would expect from the bond in a steady interest rate environment. The path of getting there is just different.
There are a couple of takeaways from the above example. First, we can mathematically compute how bond prices will change when interest rates change. When rates go up, we expect there to be downward pressure on bonds. Conversely, when rates go down, we expect prices will appreciate, which is what we saw this past quarter. A further point to this, which is often not reflected in brokerage firms’ dashboards, is the coupon payment must be included in the total return calculation.
Hopefully, this illustrates how bonds behave in a changing interest rate environment, much like we have experienced in the last few years.
When investors hold bond funds, the return calculation is based on all bond holdings in the fund. When interest rates move, the bond fund’s price will fluctuate, much like in the above example.
Despite the mathematical complexity of calculating bond fund returns, bond funds are the most efficient way to get exposure to the bond market. By holding bonds inside of a fund, you benefit from the manager’s ability to buy bonds in bulk (which can mean better pricing) and reinvest interest in a timely manner. When you see the price of the fund move, keep in mind that it is indicative of the underlying bonds’ pricing in a changing interest rate environment and that periodic losses tend to be temporary.



